Как найти дельта лямбда в оптике
Опубликовано: 26.07.2024
Формулы по темам: геометрическая оптика, интерференция, дифракция, поляризация, фотоэффект, тепловое излучение, радиоактивность, ядерные реакции и константы
* - умножение
Sqr(. ) - квадратный корень
^ - степень
Фокусное расстояние сферического зеркала
f=R/2, R – радиус кривизны зеркала
Оптическая сила сферического зеркала:
Ф=1/f
Формула сферического зеркала
1/f=1/a+1/b, где a и b - расстояния от полюса зеркала до предмета и изображения. Если изображение мнимое, то –b; если зеркало выпуклое (мнимый фокус), то –f.
Закон преломления
n1*sin(a1)=n2*sin(a2)
Предельный угол полного отражения, при переходе света из среды более оптически плотной в менее.
a=arcsin(n2/n1), n2<n1
Оптическая сила тонкой линзы
Ф=1/f=(nл/nср-1)(1/R1+1/R2), где f – фокусное расстояние линзы, nл – абсолютный показатель преломления вещества линзы, ncр – абсолютный показатель преломления окружающей среды. Радиусы выпуклых с плюсом, а вогнутых – с минусом.
Формула тонкой линзы
1/f=1/a+1/b, а – от предмета до оптического центра, b – от опт центра до изображения. Если фокус мнимый (линза рассеивающая), то –f. Если изображение мнимое, то –b.
Угловое увеличение лупы
Г=D/f, D – расстояние наилучшего зрения D=25 см.
Угловое увеличение телескопа
Г=fоб/fок, где об и ок – фокусные расстояния объектива и окуляра.
Расстояние от объектива до окуляра телескопа
L=fок+fоб, если наблюдаются удалённые объекты.
Угловое увеличение микроскопа
Г=delta*D/(fоб/fок), где delta – расстояние между задним фокусом объектива и передним фокусом окуляра.
Расстояние от объектива до окуляра микроскопа
L= fок+fоб+delta
Световой поток, испускаемый изотропным точечным источником в предел телесного угла omega.
Ф=I*omega, где I [Вт/стерадиан] - сила источника, omega=2pi(1-cos(a)), где a – угол между осью конуса и образующей. Ф[Ватт]=Ф[люмен(лм)]=Ф[кандела*стерадиан]
Полный световой поток от изотропного источника.
Ф0=4pi*I
Освещённость поверхности (светимость)
E=Ф/S, E[люкс(лк)]
Освещённость, создаваемая изотропным точечным источником
E=I*cos(a)/r^2, где а – угол падения лучей, r – расстояние до источника
Сила света любого элемента поверхности косинусного излучательного.
I=I0*cos(a), где a – угол между нормалью к эл-ту поверхности и направлением наблюдения. I0 – сила света по направлению нормали. I=[кандела(кд)]
Яркость светящейся поверхности (лучистость)
L=I/sigma, sigma – площадь проекции светящейся поверхности на плоскость, перпендикулярно направлению. L[Вт/(ср*м^2)]
Светимость
M=Ф/S, где Ф – световой поток, испускаемой поверхностью площадью S. M=[люмен/м^2]
Светимость косинусных излучателей
M=pi*L
Коэффициент отражения
ro=I’/I=((n1-n2)/(n1+n2))^2, где I’ – интенсивность отражённой
Коэффициент пропускания
tau=I’’/I=4n1*n2/(n1+n2)^2, где I’’ – интенсивность пропущенной
Если падение не по нормали
I<>I’+I’’
Ф=Ф’+Ф’’
tau=Ф’’/Ф
Скорость света с среде
v=c/n
Оптическая длина пути
L=n*l
Оптическая разность хода
Delta=L1-L2
Оптическая разность хода в плоскопараллельной пластинки 1<n1<n2
Delta=2d*Sqr(n1^2-(sin(a1))^2)-(1-n1)*lambda/2, где d – толщина пластинки, a1 – угол падения
При отражении сдвиг фазы на pi/2
Разность фаз delta колебаний
delta=2*pi*Delta/lambda0
Интенсивность двух колебаний
I=I1+I2+2*Sqr(I1*I2)*cos(delta)
Условие максимумов
Delta=+-m*lambda, тогда delta=+-2m*pi
Условие минимумов
Delta=+-(2m+1)(lambda/2), тогда delta=+-(2m+1)*pi
Условие различимости двух линий
m=lamda/Delta(Lambda)=x/Delta(x)
l(ког)=lambda^2/ Delta(Lambda)
Delta<l(ког)
Опыт Юнга
Delta=x*d/l
x=m*lambda*l/d
Бипризма Френеля
x=Delta*(a+b)/(2*Sigma*a*(n-1))
alpha=(n-1)*Sigma
Максимальное число полос
N=4*alpha^2*a*b/(lambda*(a+b))
Зеркало Ллойдя
Если прямой угол,то
Delta=2*x^2/l
Бизеркала Френеля
x=Delta*(a+b)/2*alpha*a=Delta*(b+r)/2*alpha*r, где r – от зеркала до источника, r – от пересечения зеркал до экрана, alpha – угол между зеркалами.
N=4*alpha^2*a*b/(lambda*(a+b))
Билинза Бийе
Ширина полосы
Delta(x)=lamda*f/delta, где delta – ширина вырезанного слоя.
Число полос
N=b*delta^2/(f^2*lambda), где b – расстояние до экрана от линзы.
Кольца Ньютона
Радиусы светлых колец
r=Sqr((2k-1)*R*lambda/2)
Радиусы тёмных колец
r=Sqr(k*R*lambda)
Sigma
Расстояние между полосами
(h2-h1)/x=tg(Sigma)
Sigma, где x – расстояние
Просветление оптики
Показатель преломления
n0<n1<n2
n1=Sqr(n0*n2)
Толщина плёнки
n1*d=lambda/4, обычно lambda=550 нм.
Зоны Френеля
Радиус для сферической волны
r=Sqr(a*b*m*lamda/(a+b)
Радиус для плоской волны
a->беск, r=Sqr(b*m*lambda)
Амплитуды
A=A1-A2+A3-A4+….
A=A1/2+(A1/2-A2+A3/2)+(…)=
A1/2
A(m)=(A(m-1)+A(m+1))/2
Площадь каждой зоны
S=pi*b*lambda*a/(a+b)
Площадь всех зон
S= pi*b*lambda*a*m/(a+b)
Спираль Корню
s=x*Sqr(2/(l*lambda))
Характер дифракции
p=h^2/(l*lambda), где h – размер отверстия, l – расстояние до экрана
p<<1 – дифракция Фраунгофера
p
1 - дифракция Френеля
p>>1 – геометрическая оптика
Разность фаз delta колебаний
delta=2*pi*Delta/lambda
Дифракция на одной щели
Условие минимумов
b*sin(phi)=+-m*lambda
Если под углом b*(sin(phi)-sin(phi’))= +-m*lambda
Условие максимумов
b*sin(phi)=(2m+1)*lambda/2, где phi – угол после дифракции, b – ширина щели
Если под углом b*(sin(phi)-sin(phi’)= (2m+1)*lambda/2, где phi’ – угол падения
Амплитуда
A=A0*sin(delta/2)/ (delta/2)
Интенсивность
I=I0*(sin(a))^2/a^2, где a=delta/2=pi*Delta/lambda=pi*b*sin(phi)/lambda
Дифракционная решётка
Главные максимумы интенсивности
d*sin(phi)=+-m*lambda
d*(sin(phi)-sin(phi’))= +-m*lambda, если падение под углом phi’
Главные минимумы интенсивности
a*sin(phi)=+- m*lambda
Дополнительные минимумы
d*sin(phi)=+-m’*lambda/N, где N – кол-во щелей, m’=1,2,3,4…кроме 0,N,2N…
Число главных максимумов
M=d/lamda
Амплитуда главного максимума A=A1*sin(N*gamma/2)/sin(gamma/2)
Интенсивность гл макс I=I0*(sin(delta/2))^2/(delta/2))^2
*(sin(N*gamma/2))^2/(sin(gamma/2))^2, где delta=2pi*b*sin(phi)/lambda, gamma=2pi*d*sin(phi)/lambda
Разность хода
delta*phi=lamda/(N*d*cos(phi))
Разрешающая сила
R=lambda/Delta(Lambda)=m*N
Угловая дисперсия
D(phi)=delta(phi)/delta(lambda)=m/(d*cos(phi))
Линейная дисперсия
D(l)=delta(l)/delta(lambda)
Для малых углов D(l)=
f*m/d, где f – фокусное расст собирающей линзы.
Область дисперсии (ширина спектра, там где ещё нет перекрывания спектров)
Delta(lambda)=lambda/m
Формула Вульфа-Брэгга (для пространственной дифракции)
2*d*sin(phi)=m*lambda, где phi – угол скольжения
Разрешающая сила объектива
R=1/beta=D/(1.22*lambda), где beta – угловое расстояние, D – диаметр объектива
Угол Брюстера (под которым, отраж волна полностью поляризуется)
tg(a)=n2/n1
Интенсивность естественного света после прохождения поляризатора
I=I0/2
Интенсивность после прохождения анализатора (закон Малюса)
I=I0*(cos(a))^2
Степень поляризации
P=(Imax-Imin)/(Imax+Imin)
Разность фаз между max и min pi/2
Коэффициент отражения света, плоскость поляризации перпендикулярна плоскости падения
ro=I’/I=(sin(a1-a2))^2/( sin(a1+a2))^2, где a1 – угол падения, а2 – угол преломления
если параллельна,то
ro=I’/I=(tg(a1-a2))^2/( tg(a1+a2))^2
Двупреломляющая пластинка
Delta=h(n(o)-n(e))
Пластинка в четверть волны (превращает циркулярный в плоский и обратно)
h|n(o)-n(e)|=m*lambda/4, m – нечётная, вносит доп разность ходам m*pi/2
Пластинка в половину волны (плоскость поляризации ортогонализируется)
h|n(o)-n(e)|=m*lambda/2, m – нечётная, вносит доп разность ходам m*pi
Анизотропное тело
n(o)-n(e)=k*sigma, где sigma – напряжение, к – зависит от в-ва
Эффект Керра
n(e)-n(o)=B*lambda*E^2
Эффект Коттона-Муттона
n(e)-n(o)=С*lambda*H^2
Оптически активные в-ва
Твёрдые тела
phi=alpha*d, d – путь света в в-ве.
Чистые жидкости
phi=[alpha]*ro*d, [alpha] – удельное вращение
Растворы
phi=[alpha]*С*d, С – концентрация
Эффект Фарадея
phi=V*d*B, B – магнитная индукция, V – постоянная Верде
Поляризация рассеянного света
I=I0*(1+(cos(Phi))^2), phi – угол рассеяния
dn/d(lambda)<0 – нормальная дисперсия
dn/d(lambda)>0 – анормальная дисперсия
n=Sqr(epsilon) – в изотропной немагнитной среде
epsilon=1+P(t)/(epsilon0*E(t)), P(t)=n0*p, p=-q*x,
epsilon=1+b/(omegao0^2-omega^2), b=n0*q^2/(epsilon0*m)=N0*qe^2/(epsilon0*m), где N0 – концентрация электронов, n0 – концентрация диполей, m – масса эл облака.
Закон Бугера (поглощение света)
I=I0*exp(-a*x), а – толщина слоя 1/a, после кот I падает в е-раз, x – толщина слоя
Ф=Ф0*exp(-a*r), r – радиус сферического слоя
Оптика движущихся тел
Эффект Доплера в релятивистском случае
nu=nu0*sqr(1-beta^2)/(1+beta*cos(a)), beta=v/c, a – угол между v и наблюдателем, nu0 – собственная частота излуч неподвижным источником
Если движение по прямой
Источник удаляется (nu=0)
nu=nu0*sqr((1-beta)/(1+beta))
Источник приближается (nu=pi)
nu=nu0*sqr((1+beta)/(1-beta))
Эффект Доплера в нерелятивистском случае
Delta(nu)/nu=v*cos(nu)/c
Эффект Вавилова-Черенкова
cos(a)=v/(n*c)=1/beta*n
Законы теплового излучения
Закон Стефана-Больцмана
M(e)=sigma*T^4
sigma – постоянная Стефана-Больцмана = 5.67*10^-8 Вт/(м^2*K^4)
Энергетическая светимость серого тела
M(e)=epsilon*sigma*T^4, epsilon – степень черноты (коэф теплового излучения)
Закон смещения Вина
lambda(m)=b/T, b – постоянная Вина = 2.9*10^-3 м*К
Формула Планка
M(lambda,T)=2pi*h*c^2/(lambda^5*(exp(hc/lambda*k*T-1))
M(omega,T)=h(с чертой)*omega^3/(4*pi^2 *c^2*(exp(h(c чертой)*omega/ k*T-1))
M – спектральная плотность, к – пост Больцмана =1.38*10^-23 Дж/К
M(lambda, T)max=C*T^5, C=1.3*10^-5 Вт/(м^3*К^5)
R(nu,T)=R(lambda,T)*d(lambda)/d(nu)=R(lambda,T)*lambda^2/c
Спектральная поглощательная способность
A(nu, T)=d(Wпогл)/d(W)
Закон Кирхгофа
r(nu,T)=R(nu,T)/A(nu,T) – универсальная ф-ия Кирхгофа
Формула Рэлея-Джинса
M(nu,T)=2pi*nu^2*<epsilon>/c^2=2pi*nu^2*k*T/c^2
Формула Вина
R(nu,T)=C1*nu^3*exp(-C2*nu/T), где C1 и С2 - константы
Для чёрного тела R=M=r
sigma=2pi^5*k^4/(15*c^2*h^3) (получается интегрированием ф-лы Планка по частотам.
b=T*lambda(max)=hc*/(4.965*k) - Закон смещения Вина получается при анализе ф-лы Планка на экстремум
Формула Эйнштейна
В общем случае
E=h*nu*A+Tmax, где A – работа выхода электрона из металла, Тmax – максимальная кинетическая энергия фотоэлектрона, Е – энергия падающего фотона
В случае, если h*nu>>A
h*nu=Tmax
h*nu=qe*U=qe*(U2-U1)
Максимальная кинетическая энергия фотона
Нерелятивистский случай (h*nu
5 кэВ)
Tmax=m0*v^2max/2, m0 –масса покоя электрона
Релятивистский случай (h*nu>>5 кэВ)
Tmax=(m-m0)*c^2=m0*c^2*(1/sqr(1-beta^2)-1), beta=vmax/c, m –масса релятивистского электрона
Красная граница фотоэффекта
lambda0=hc/A; nu0=A/h, lambda0 – максимальная длина волны излучений, при которых ещё возможен фотоэффект
Задерживающая разность потенциалов
U=U2+|U1|=U2-U1, U1<0
T=qe*U=qe*(U2-U1)
Давление света при нормальном падении
p=Ec(1+ro)/c=omega*(1+ro), Ec – облучённость поверхности, omega – объёмная плотность энергии излучения, ro – коэффициент отражения
Эффект Комптона
Delta(lambda)=lambda’-lambda*h(1-cos(a))=2h*(sin(a/2))^2/(m*c)=2*lambdaC*(sin(a/2))^2, a – угол рассеяния фотона, lambdaC – комптоновская длина волны
lambdaC=h/(m*c)=2.435*10^-12 м (при рассеянии на электронах)
E(gamma)<100 кэВ – фотоэффект
E(gamma)
500 кэВ – эффект Комптона
E(gamma)>10 МэВ – образование электрон-позитронных пар
Атом водорода по теории Бора
Момент импульса
L=m*v*r=n*h(с чертой)
Z*qe^2*k/r^2=me*v^2/r
Радиус n-ой орбиты
rn=n^2*h^2/(Z*qe^2*me)
Скорость
v=qe^2/(2*h*n*epsilon0)
Частота
nu=qe^2*me/((n*h)^3*4*epslon0^2)
Полная энергия электрона
E=-k*Z*qe^2/2r=-Z^2*me*qe^4/(n^2*8h^2*epsilon0^2), epsilon0=8.85*10^-12 Ф/м
Формула для расчёта поглощения и излучения атома
1/lambda=R/c*Z^2*(1/n^2-1/m^2), n – куда переходит электрон, m – откуда переходит электрон
R=me*qe^4/(8*h^3*epsilon0^2)=3.29*10^-15 1/c
nu=Z^2*R*(1/n^2-1/m^2)
Энергия
H*nu=En-Em=Z^2*h*R*(1/n^2-1/m^2)
E=Z^2*Ei*(1/n^2-1/m^2), Еi – энергия ионизации Ei=h*R=13.6 эВ (для H)
Коротковолновая граница рентгеновского спектра
lambda(min)=h*c/(|qe|*U)
Закон Мозли
nu=R(Z-sigma)^2*(1/n^2-1/m^2), R=2.07*10^16 с^-1
Для Kalpha линий
omega(Kalpha)=3R*(Z-1)^2/4
1/lambda(Kalpha)=3R’*(Z-1)^2, R’=1.10*10^7 м^-1
Радиус ядра
r=r0*A^(1/3), r0=1.4*10^-15
Объём шара
V=4pi*R^3/3
Площадь шара
S=4pi*R^2
Средняя плотность ядерного вещества
<ro>=A*m/Vя, где m=1 а.е.м.=1.66*10^-27 кг
Молярная масса смеси двух компонентов
M=(m1+m2)/(m1/M1+m2/M2)=M1*M2/(omega1*M2+omega2*M1), где omega – массовая доля, omega1=m1/(m1+m2)
Закон ослабления gamma излучения
Ослабление плотности потока
J=J0*e^(mu*x), x – толщина, mu – линейный коэффициент, J0 – плотность падающего излучения
Ослабление интенсивности излучения
I=I0*e^(mu*x)
Толщина слоя половинного ослабления (ослабление в 2 раза)
x=ln2/mu
Доза излучения (поглощённая)
D=Delta(W)/Delta(m), Delta(W) – энергия ионизирующего излучения, переданная эл-ту, Delta(m) – масса эл-та. D=[Грей(Гр)]=[Дж/К]
Мощность дозы излучения
D’=Delta(D)/Delta(t)
Экспозиционная доза излучения
X=Delta(Q)/Delta(m), Delta(Q) – сумма зарядов созданных электронов в процессе ионизации. X=[Рентген(Р)]=[Кл/кг]
Мощность экспозиционной дозы
X=Delta(X)/Delta(t)
Экспозиционная доза при падении на экранированный слой толщиной x
X=X0*e^(-mu*x), X0 – эксп. доза при отсутствии слоя.
Эксп. доза излучения падающего за время t на объект на расстоянии R от точечного ист
X=X’*t/R^2
a/zX, где a – массовое число (число нуклонов в ядре), z – число протонов, n=a-z – число нейтронов
Альфа-распад
a/zX=(a-4)/(z-2)Y+4/2He
beta-распад электронный
a/zX=a/(z+1)Y+0/-1e+0/0nu
1/0n=1/1p+0/-1e+0/0nu
beta-распад позитронный
a/zX=a/(z-1)Y+0/1e+nu
1/1p=1/0n+0/1e+nu
beta-распад (К-захват)
a/zX+0/-1e=a/(z-1)X+0/0nu
1/1p+0/-1e=1/0n+0/0nu
Ядерная реакция под действием alpha
a/zX+4/2He=(a+3)/(z+1)Y+1/1H
Аннигиляция
0/-1e+0/+1e=2*gamma
Рождение
gamma+X=X+0/-1e+0/1e
Законы сохранения
A, Z, E, p
Энергия ядерной реакции
Q=c^2*[(m1+m2)-(m3+m4)]
Q=(Т1+Т2)-(Т3+Т4)
Эндотермическая T3+T4>T1+T2
Экзотермическая T3+T4<T1+T2
Дефект массы
Delta(m)=(m1+m2+m3….)-m
Для атомного ядра дефект массы
Delta(m)=(Z*mp+N*mn)-mя
Энергия связи
Eсв=c^2*Delta(m)
Удельная энергия связи
Eуд=Eсв/A
Радиоактивность
N=N0*exp(-lambda*t), N – число нераспавшихся атомов, N0 – изначально кол-во атомов, lambda-постоянная радиоактивного распада
Период полураспада
T1/2=ln2/lambda=0.683/lambda
Число атомов, распавшихся за время t
Delta(N)=N0-N=N0(1- exp(-lambda*t))
При Delta(t)<<T1/2
Delta(N)
lamda*N*Delta(t)
Среднее время жизни ядра
tau=1/lamda
Число атомов, содержащихся в радиоактивном изотопе
N=m*NA/M, NA – число Авогадро, NA=6.02*10^23 моль^-1
Активность
A=-dN/dt=lambda*N=lambda* N0*exp(-lambda*t)
Активность изотопа в начальный момент времени
A0=lambda*N0
Активность изотопа со временем
A=A0* exp(-lambda*t)
Массовая активность
a=А/m
Смесь изотопов
lambda1*N1=lambda2*N2=lambda3*N3=…
Волны Де-Бройля
Длина волны
lambda=h/p=h/sqr(2m*K), K=150 эВ, длина волны электрона 1А
Фазовая скорость
vфаз=omega/k=E/p=c^2/v
Групповая скорость
u=dE/dp
для свободной частицы
E=Sqr(m^2*c^4+p^2*c^2); u=v
Принцип неопределённости
Delta(x)*Delta(p)>=h (h/2)
Delta(E)*Delta(t)>=h
___________
Константы
Диапазон света
Инфракрасный 1мм-0,76 мкм,
Видимый – 0,76-0,40 мкм
Ультрафиолетовый – 0.40-0,01 мкм
|e|=p=1.6*10^-19 Кл
m(e)=9.1*10^-31 кг=0.00055 аем
m(p)=1.6726*10^-27 кг=1.00728 аем
m(n)=1.6749*10^-27 кг=1.00867 аем
m(d)=3.35*10^-27 кг=2.01355 аем - Дейтон
m(alpha)=6.64*10^-27 кг=4.00149 аем
Е0(e)=8.16*10^-14 Дж=0.511 МэВ
E0(p)=1.5*10^-10 Дж=938 МэВ
E0(n)=1.51*10^-10 Дж=939 МэВ
E0(d)=3*10^-10 Дж=1876 МэВ
E0(alpha)=5.96*10^-10 Дж=3733 МэВ
Солнечная постоянная
C=1.4 кДж/(м^2*c)
Молярная газовая постоянная
R=kN(a)=8.31 Дж/(моль*К)
Гравитационная постоянная
G=6.672*10^-11 Н*м^2кг^2
Число Авогадро
N(a)=6.022*10^23 моль^-1
k=1/(4pi*e*e(0))=9*10^9 Н*м^2/Кл^2
Постоянная Больцмана (термодинамика)
k=1.3807*10^-23 ДжК
Электрическая постоянная
e(0)=8.854*10^-12 Фм (или Кл/(Н*м^2))
Магнитная постоянная
mu(0)=4pi*10^-7=1.257*10^-6 Гнм (или Н/А^2)
1 аем=1.66*10^-27 кг=931.5 МэВ
Постоянная Планка
h=6.626*10^-34 Дж*с
Постоянная Ридберга
R’=1.1*10^7 м^-1
R=3.29*10^15 с^-1
Постоянная Фарадея
F=9.648*10^4 Кл/моль
Магнетон Бора
mu(B)=9.27*10^-24 Дж/Тл
Ядерный магнетон
mu(N)=5.05*10^-27 Дж/Тл
Постоянная Стефана-Больцмана
sigma=5.67*10^-8 Вт/(м^2*К^4)
Стандартный объём
V=22.4*10^-3 м^3/моль
Энергия ионизации атома водорода
Ei=13.6 эВ
Спектральным анализом называют метод определения состава вещества в зависимости от его спектра. Этот метод был предложен в XIX веке Бунзеном и Кирхгофом. Этот метод базируется на том, что:
Атомные спектры разных химических элементов не похожи друг на друга.
Линейчатые спектры не связаны с тем, каким способом атомы вещества приходят в возбуждение. Они зависят только от свойств атомов.
Используя спектральный анализ, есть возможность найти элемент в составе сложного вещества, если его масса весьма мала (порядка $<10>^<-10>г$).
В настоящее время существуют таблицы спектров, которые включают спектры всех известных на сегодняшний момент атомов.
Спектр излучения молекул состоит из широких размытых полос, не имеющих четких границ. Такие спектры называют полосатыми. Спектр излучения атома имеет отличающийся вид. Он образован отдельными, четкими линиями. Спектры атомов называют линейчатыми. Для любого атома имеется определенный линейчатый спектр. В свою очередь линии в спектрах расположение линий в спектрах является закономерным. Первые удачные шаги в подборе формул, которые бы правильно описали расположение спектральных линий, сделал Бальмер. Он исследовал спектр атома водорода.
Помощь со студенческой работой на тему
Спектральный анализ в оптике
Спектральный анализ находит применение для:
Исследования составов веществ, поиска новых элементов.
Определения состава небесных тел.
Контроля над составом веществ в различных отраслях промышленного производства.
Определения состава руд и минералов в геологии.
Исследуя спектры, в астрофизике вычисляют температуры небесных светил, скорости их перемещения, давление и т.д.
Спектральные приборы и их характеристики
К спектральным аппаратам относят приборы, которые позволяют определять длины волн или их разницу двух близких спектральных линий (дифракционная решетка, эшелон Майкельсона и т.д). Характеризуют подобные устройства с помощью следующих физических величин.
Дисперсия спектрального аппарата ($D$). Как правило, положение линии спектра задают углом, относительно нормали к фронту волны после ее дисперсии. Потому дисперсию определяют как угловое расстояние между направлениями для двух спектральных линий, которые отличаются на $1$ ангстрем относительно длины волны:
где $\delta \lambda $ -- разница длин волн соседних линий спектра, $\delta \varphi $ -- разница в углах. В выражении (1) имеется в виду угловая дисперсия. Тогда как линейная дисперсия ($D'$) определена как:
где $\delta s=f\delta \varphi$ -- линейное расстояние между линиями спектра, $f$ -- фокусное расстояние линзы, которая проецирует спектр на экран.
Разрешающая способность спектрального прибора. Имеющаяся дисперсия не обеспечивает возможности раздельного наблюдения двух близких спектральных линий ($<\lambda >_1\ и\ <\lambda >_2$). В любом приборе переход от максимума данной длины волны к минимуму идет постепенно, что зависит от устройства аппарата. Для того, чтобы спектральный прибор мог разрешить две длины волны (установить существование спектральных линий двух длин волн) надо чтобы при заданном расстоянии между максимумами рисунок исследуемых линий был четким. Возможность различия таких максимумов в этом случае зависит от чувствительности к контрасту метода, который применяют для исследования интенсивности по спектру. Рэлей предложил считать разрешение полным, если максимум первого «горба» совпадает с минимумом второго «горба».
Мерой разрешающей способности ($R$) спектрального аппарата считают отношение длины волны ($\lambda $) около которой идет измерение к минимальному интервалу ($\delta \lambda $), который может прибор различить:
Так, для дифракционной решетки имеем:
где $N$ -- число штрихов, $Nd$- общая ширина решетки.
Область дисперсии ($G$). Так как в действительности на практике имеют дело с немонохроматическим светом, а некоторым спектральным участком (от $\lambda $ до $\lambda +\triangle \lambda $), присутствие подобного состава длин волн вносит существенные проблемы при работе спектральных аппаратов. Особенно тех, в которых исследуются спектры высоких порядков, которые могут взаимно перекрывать друг друга. Так, у каждого прибора имеется предельная ширина спектрального интервала $\triangle \lambda $, при которой имеется возможность получить дискретные максимумы и минимумы. Этот интервал и называется дисперсионной областью. Для дифракционной решетки имеем:
Так, дифракционная решетка имеет разрешающую способность близкую к разрешающей способности неплохих интерференционных спектроскопов, но более применима.
С помощью спектрального аппарата сложный волновой импульс разлагается в спектр, что означает, что установление распределения энергии, которая сосредоточена в этом импульсе по разным частотам. Но при этом характер распределения энергии по частотам для разных приборов различен. Получается, что результат излучения импульса спектральным прибором зависит от свойств импульса и от свойств спектрального прибора.
Задание: Имеются две дифракционные решетки длины $l=10\ мм$ с разными периодами: $d_1=2\ мкм$ и $d_1=4\ мкм.$ Каково отношение разрешающих способностей этих решеток для длины волны равной $644$ нм?
Решение:
В качестве основы для решения задачи примем условие максимумов для дифракционной решетки:
\[dsin\varphi =m\lambda ,\ где\ m-целые\ числа\ \left(1.1\right).\]
Учтем, что $<\left(sin\varphi \right)>_
Для того чтобы использовать выражение для вычисления разрешающей способности дифракционной решетки:
Следует найти число штрихов решеток как:
Из выражений (1.3) и (1.4) следует, что:
Ответ: Не проводя вычислений можно сказать, что $R_
Задание: Чему равна угловая дисперсия для угла дифракции $\varphi =30^\circ $ для спектра третьего порядка (m=3), если дифракционная решетка имеет $N=1000$ штрихов и постоянную $d=<10>^<-5>м$.
Решение:
За основу решения задачи примем определение дисперсии спектрального прибора:
Интерференция — такое наложение волн, при котором происходит их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн.
Необходимые условия для наблюдения интерференции:
1) Волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени;
2) Волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции. Волны, для которых выполняются эти два условия, называются когерентными .
При наложении когерентных волн возможны два предельных случая:
1) Условие максимума :
Разность хода волн равна целому числу длин волн (иначе четному числу длин полуволн). \[d_2=d_1=2k\dfrac<\lambda><2>\] где ( \(k=0, \pm 1,\pm 2, \pm 3. \) ). В этом случае волны в рассматриваемой точке приходят с одинаковыми фазами и усиливают друг друга –– амплитуда колебаний этой точки максимальна и равна удвоенной амплитуде.
2) Условие минимума :
Разность хода волн равна нечетному числу длин полуволн. \[d_2=d_1=(2k+1)\dfrac<\lambda><2>\] где ( \(k=0, \pm 1,\pm 2, \pm 3. \) ). Волны приходят в рассматриваемую точку в противофазе и гасят друг друга. Амплитуда колебаний данной точки равна нулю.
Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.
Дифракция волн — явление отклонения волны от прямолинейного распространения и огибания волной препятствия.
При дифракции происходит искривление поверхности волны у краев препятствия. Особенно явно дифракция проявляется в том случае, если размеры препятствия сравнимы с длинами волн.
Явление дифракции можно объяснить при помощи принципа Гюйгенса, так как любую точку поля волны следует рассматривать как источник вторичных волн, которые распространяются по всем направлениям, в том числе и в область геометрической тени препятствия.
В прозрачной плоской дифракционной решетке (см. рисунок) ширина прозрачного штриха равна \(a\) , ширина непрозрачного промежутка — \(b\) . Величина \(d=a+b=\dfrac<1>

Пусть плоская монохроматическая волна падает нормально к плоскости решетки. По принципу Гюйгенса-Френеля каждая щель является источником вторичных волн, способных интерферировать друг с другом. Получившуюся дифракционную картину можно наблюдать в фокальной плоскости линзы, на которую падает дифрагированный пучок.
Допустим, что свет дифрагирует на щелях под углом \(\varphi\) . Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного направления \(\varphi\) будут одинаковыми в пределах всей дифракционной решетки:
В тех направлениях, для которых разность хода равна четному числу полуволн, наблюдается интерференционный максимум. Наоборот, для тех направлений, где разность хода равна нечетному числу полуволн, наблюдается интерференционный минимум. Таким образом, в направлениях, для которых углы \(\varphi\) удовлетворяют условию
наблюдаются главные максимумы дифракционной картины. Эту формулу называют формулой дифракционной решетки. В ней \(m\) называется порядком главного максимума. Между главными максимумами располагается \((N - 2)\) слабых побочных максимумов, но на фоне ярких главных максимумов они практически не видны. При увеличении числа штрихов \(N\) главные максимумы, оставаясь на прежних местах, становятся более резкими.
При наблюдении дифракции в белом свете все главные максимумы, кроме нулевого центрального максимума, окрашены. Это объясняется тем, что, как видно из формулы \[\sin\varphi=\dfrac
Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше — область ультразвука.
К основным характеристикам звука относятся громкость и высота. Громкость звука определяется амплитудой колебаний давления в звуковой волнеиизмеряется в специальных единицах — децибелах (дБ). Чем больше амплитуда колебаний в звуковой волне, тем громче звук.
Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах — больше, чем в жидкостях.
Дифракционная решетка - оптическое устройство, представляющее собой совокупность большого числа параллельных щелей, равноудаленных друг от друга.
Суммарная ширина щели и штриха (a+b=d) – период решетки.
! d=((a+b)*N)/N=C/N!, где С –ширина решетки, N -число штрихов на ней.

на нем: Л- линза; Р – решетка; Э - экран
Максимумы, которые образуются на экране, после интерференции вторичных волн, идущих от узких щелей, удовлетворяют условию:
!d*sin фи = k*лямбда! - формула дифракционной решетки.
фи - угол дифракции (угол отклонения от прямолинейного направления);
k - порядок спектра;
лямбда - длина волны света, освещающего решетку,
Дифракционные спектры для монохроматического света представляет собой чередование максимумов и минимумов по обе стороны от центрального механизма. Максимумы имеют цвет соответствующей длины света, освещающего решетку.
Если решетку освещать белым светом, то центральный максимум будет белым, а остальные будут представлять собой чередование цветных полос плавно переходящих друг в друга, т. к. sin фи= k*лямбда/d - зависит от длины волны света. D = к/t - угловая дисперсия решетки. R =k*N - разрешающая способность.
Диффузия в жидкости. Уравнение Фика. Уравнение диффузии для мембран.
Диффузия - самопроизвольное проникновение молекул одного вещества между молекулами других.
Явление диффузии - важный элемент диффракционирования мембран. При диффузии происходит перенос массы вещества. В биофизике это называется транспорт частиц. Основным уравнением диффузии является уравнение Фика:
где I – плотность частиц при диффузии в жидкость.
D – коэффициент диффузии.
Коэффициент 1/3 возник ввиду трехмерного пространства и хаоса в движении молекул (в среднем в каждом из 3-х направлений перемещается 1/3 часть всех молекул)
сигма - средняя длина свободного пробега молекул
тау -среднее время оседлой жизни молекул
С- массовая концентрация молекул
Х- перемещение молекул вдоль оси X
- градиент массовой концентрации
Знак «-» показывает, что диффузия молекул происходит из области их большей концентрации в область меньшей концентрации.
Уравнение диффузии можно записать в виде:
n – концентрация молекул.
Градиент концентрации
R- универсальная газовая постоянная; Т- абсолютная температура градиент химического потенциала,
Тогда
С - концентрация частиц. А Эйнштейн показал, что D пропорционально Т. Дня биологических мембран уравнение Фика имеет вид:
- концентрация молекул внутри клеток
- коэффициент проницаемости
l – толщина мембраны.
Дифракция света на щелях.
Дифракцией света называют явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями.
Описать картину дифракции можно с учетом интерференции вторичных волн.

Рассмотрим дифракцию от узкой щели (АВ)
MN – непрозрачная преграда;
АВ=а – ширина щели;
АВ – часть волновой поверхности, каждая точка которой является источником вторичных волн, которые распространяются за щелью по разным направлениям. Линза соберет лучи А, А1 и В в точке О1 экрана.
АD - перпендикуляр к направлению пучка вторичных волн. Разбили ВD на отрезки =лямда/2.
АА1, А1В - зоны Френеля. Вторичные волны, идущие от двух соседних зон Френеля, не гасят друг друга, так как отличаются по фазе на пи. Число зон, укладывающихся в щели, зависит от длины волны лямда и угла альфа.
Поэтому на экране получится система светлых (mах) и темных (min) полос симметричных относительно центра (альфа=треугольник - изменение) - наиболее яркой полосы.
Интенсивность остальных максимумов убывает с увеличением к.
3аконы излучения абсолютно чёрного тела (Стефана - Больцмана, Вина). Формула Планка. Использование термографии в диагностике.
Излучение чёрного тела имеет сплошной спектр. Графически это выглядит для разных температур так:
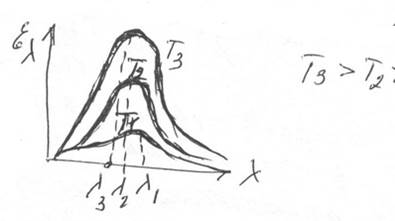
Существует максимум спектральной светимости, который при повышении
температуры смещается в сторону коротких волн.
По мере нагревания чёрного тела его энергетическая светимость (Re)
увеличивается: Re = опред интеграл от 0 до бескон от Eлямда*dлямда
Стефан и Больцман установили, что Re=сигма*T^4
Сигма = 5,6696*10^-8 Вт/K*м^2 - постоянная Стефана-Больцмана,
T=t+273 - абсолютная (термодинамическая) температура по шкале
Кельвина. Все замечали это на практике, чем выше температура спирали, нагретой печи, тем больше они излучают тепла.

Планк получил формулу для спектральной плотности абсолютно черного тела (Eлямда) и серого тела (r лямда) (лямда-индекс): Eлямда=2п*h*c^2/лямда^5 * 1/exp[h*c/k*T*лямда-1]
альфа - коэффициент поглощения
h - постоянная Планка;
С - скорость света в вакууме;
лямда - длина волны;
k - постоянная Больцмана;
Т - абсолютная температура.
2 Затухающие колебания и декремент затухания. Апериодические колебания.
Свободные колебания (происходящие без внешнего воздействия периодически действующей силы) являются затухающими. График затухающих колебаний имеет вид:

Амплитуда колебаний с каждым разом убывает. Затуханию способствуют силы трения и сопротивления, возникающие в средах. Пусть r-коэффициент трения, характеризующий свойство среды оказывать сопротивление движению. Тогда БЕТТА= r/2m – коэффицент затухания.
Wo= корень(K/m) – циклическая частота собственных колебаний, тогда W^2=Wo^2-БЕТТА^2, где W – циклическая частота затухания колебаний.
Быстрота затухания колебаний определяется коэффициентом затухания. Уравнение затухающих колебаний имеет вид А=Ао*l в степени минус бета*t
Ao – первоначальная амплитуда, А-амплитуда затухающих через время t.
Лямда=lnA(t)/A(t+T)=lnAo*(e в степени минус бета*t)/Ao*e^-бета*(t+T)=ln(e^ бета*t) –логарифмический декрет затухания.
!Лямда=бета*Т!- связь логарифмического декремента затухания с коэффициентом затухания. При сильно затухании колебания становятся апериодическими (если бета^2>Wo^2)
№31 Импеданс полной цепи переменного тока. Сдвиг фаз. Резонанс напряжения.
Рассмотрим последовательно соединенные R, L, C.
При последовательном соединении:

1) Uвх=U0*cosW*t=Ur+Ul+Uc – входное напряжение.
2) I=I0*cos(W*t-фи) – сила тока в цепи.
Начертим векторную диаграмму:

Ur0 – совпадает по фазе с силой тока;
Ul0 – опережает на пи/2;
Uc0 – отстает от тока на пи/2.
По теореме Пифагора: (U0)^2=(U0r)^2+(U0l-U0c)^2
Сократив обе части уравнения на (I0)^2 получим выражение для полного сопротивления (Z):
Z=квадратный корень из (R^2+(W*L-1/W*c)^2) – импеданс.
Если сопротивление катушки Xl= W*L равно сопротивлению конденсатора Xc=1/W*c, то полное сопротивление Z=R; по закону Ома Iрез=U0/Z=U0/R (Iрез – резонансный ток) – сила тока резко возрастает – РЕЗОНАНС. При этом Ul=Uc>>U0 – резонанс напряжений. Это возможно, т.к. Ul и Uc сдвинуты по фазе между собой на пи:

При этом на резисторе R выделяется максимальное количество теплоты:
№32 Импенданс тканей организма. Эквивалентная Электрическая схема. Оценка жизнеспособности тканей и органов но частотной зависимости к углу сдвига фаз.
Ткани организма проводят как постоянный так и переменный ток. Биологическая мембрана а значит и весь организм обладает емкостным сопротивлением, т.к. обладают емкостью, т.е. способны
накапливать заряд. При пропускании через живые ткани переменного тока наблюдается отставание напряжения от тока. Омические емкостные свойства биологических тканей можно моделировать используя эквивалентные электрические схемы, при любых частотах зависимость сдвига фаз и импенданса от частоты выполняется для схемы
1/Zв2=1/Rв2+1/корень(R1 в2+1/Wв2*Св2)!, где Z-полное сопротивление данной цепи, с - ёмкость.
При малых частотах: Z=R2 При больших частотах: Zmin=(R1*R2)/(R1+R2).

Графическое изображение зависимости импенданса живой ткани от частоты переменного тока.
Сдвиг фаз между током и напряжением tg фи = R/Xc=RWC (1).

Частотная зависимость сдвига фаз живой ткани. При отмирании ткани натрий-калиевый канал биологических мембран разрушается, цитоплазма
клетки (проводник) соединяется с межклеточной
жидкостью(проводник) и емкостные свойства ткани уменьшаются, а это значит, что и импенданс (Z) и сдвиг фаз (фи) меньше зависят от частоты. Мёртвая ткань обладает лишь омическим сопротивлением (R), и не зависит от частоты. Диагностический метод, основанный на регистрации изменения импенданса тканей и сдвига фаз называется РЕОГРАФИЕЙ.
Коэффициент дельта – это уровень изменений производного инструмента к стоимости базового инструмента (ценной бумаги, валюты, наличного товара и так далее).
Сущность коэффициента дельта
В практике опционной торговли коэффициент дельта отображает, в какой степени стоимость опциона реагирует на изменение курсовой цены акции в суммарном виде. Другими словами, дельта показывает, как реально изменится опцион, если стоимость акции возрастет на один процент.
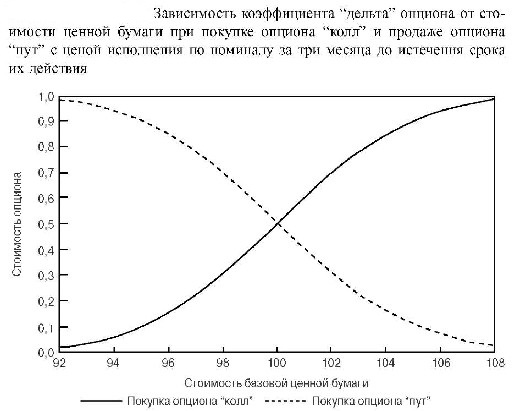
Как правило, параметр коэффициента дельта для опционов колл имеет фиксированные границы – от нуля до единицы. Если покупка опциона на определенный актив выгоднее, чем сделка с самим финансовым инструментом в его основе, то показатель дельта будет стремиться к единице. Такой параметр свидетельствует, что любой суммарный доход на акцию гарантирует приблизительно такой же уровень прибыли и на опцион.
Если же стоимость исполнения опциона намного больше уровня «call» или ниже «put» базового финансового актива в его основе, то в таком случае коэффициент дельта будет стремиться к «нулю». Подобный параметр свидетельствует, что рыночная цена акции фактически не влияет на стоимость производного инструмента.
Расчет коэффициента дельта
В большинстве случаев расчет дельта коэффициента осуществляется для инвестиционного портфеля в целом. При этом в состав такого портфеля могут входить не только опционы, но и ряд других производных ценных бумаг, зависящих от базового финансового инструмента. В этом случае расчет коэффициента дельта производится по формуле:
где П – это общая цена инвестиционного портфеля, а dS – общая стоимость активов.
Применение коэффициента дельта
На фондовом рынке коэффициент дельта широко применяется при работе с производными инструментами. К примеру, он полезен для хеджирования фьючерсных контрактов (дельта-хеджирование). При проведении операции дельта-хеджирования трейдер должен купить фьючерсные контракты, то есть открыть длинную позицию. Вопрос лишь в том, какое число контрактов ему понадобится.
Если коэффициент дельта равен 0,5, то покупателю потребуется пять фьючерсных контрактов, каждый из которых обойдется в сумму 19 долларов. Что касается параметра дельты для фьючерсов, то он будет в диапазоне от -1 до +1. При этом позиция трейдера принимает следующий вид:
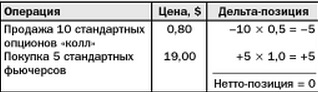
Если по завершению срока действия опциона стоимость фьючерса останется на том же уровне, что и в момент покупки, то коэффициент дельта также не изменится. При этом покупатель не будет исполнять опцион. В такой ситуации оптимальный вариант для трейдера – закрыть свою фьючерсную позицию путем продажи контрактов по цене в 19 долларов США. В этом случае прибыль участника достигает величины полученной премии – 8 тысяч долларов США. Эта ситуация представляет собой идеальный хедж, который в реальности случается крайне редко. Давайте рассмотрим несколько примеров.
До завершения срока действия опциона рыночная стоимость фьючерсов достигает уровня 19,5 долларов США. В свою очередь коэффициент дельта возрастает до +0.6. Чтобы сберечь нейтральную позицию трейдер должен купить шесть фьючерсных контрактов. Таким образом, трейдер покупает еще один контракт и тратит еще 19,5 долларов США. Итог следующий:
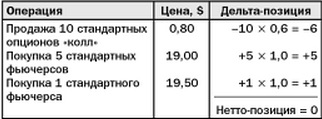
Так как стоимость фьючерсов возросла, по завершении срока опционов покупатель может воспользоваться правом покупки базового актива. Для постановки десяти фьючерсных позиций (в данном случае длинных) по девятнадцать долларов каждая, трейдер покупает фьючерсы по цене 19,5 долларов.
В этом случае затраты покупателя следующие:
Цена фьючерсов подскакивает до уровня 22 долларов США, а коэффициент дельта становится 0.9. В такой ситуации для поддержания «нейтральности» трейдеру потребуется целых десять фьючерсов. По завершении сроков действия опционов, позиции участника рынка будут выглядеть следующим образом:
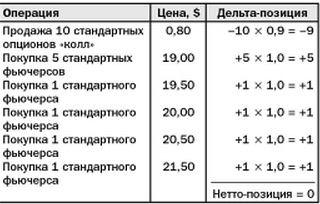
В таком случае трейдер обязательно воспользуется своим правом по завершении срока опциона купить базовый актив. При этом для поставки десяти фьючерсных позиций под девятнадцать долларов трейдер вынужден покупать фьючерсы по двадцать два доллара.
Здесь затраты трейдера следующие:
В этом случае доход составляет 15 тысяч долларов (5*3*1000), 2,5 тысячи долларов (1*2,5*1000), 2 тысячи долларов (1*2*1000), 1,5 тысяч долларов (1*1,5*1000) и 500 долларов (1*0.5*1000).
В итоге суммарная операционная премия трейдера составит 8 тысяч долларов, а убыток – 500 долларов.
Хеджирование с учетом коэффициента дельте позволяет трейдеру свести свои затраты к минимуму. В обычном случае покупатель получил бы убыток равный 30 тысячам долларов.
Крупная компания-инвестор в США занимает три позиции по опционам на австралийский доллар. Особенности сделки следующие:
Теперь можно посчитать общий коэффициент для портфеля, который составит:
1000 тысяч * 0.533 – 200 тысяч *0.468 – 50 тысяч * (-0.508) = -14,9 тысяч долларов.
Данный расчет показывает, что инвестиционный портфель может быть нейтральным, если инвестор займет длинную позицию на 14.9 тысяч австралийских долларов.
Есть еще один вариант достижения дельта-нейтральности портфеля – при помощи 6-ти месячного форвардного контракта. Суть в следующем. К примеру, на территории Австралии безрисковая ставка составляет 8% в год. На территории США этот же параметр составляет 5%. Таким образом, параметр r = 0.05, а параметр rf = 0.08.
Wikimedia Foundation . 2010 .
буква — Знак (азбучный), письмена (множ. ч.), иероглиф (гиероглиф), каракуля, руны. Нагородил какие то каракули, и читай. .. Ср. знак. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. буква … Словарь синонимов
Буква Л — Буква кириллицы Л Кириллица А Б В Г Ґ Д … Википедия
лямбда — сущ., кол во синонимов: 1 • буква (103) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Лямбда — Греческий алфавит Αα Альфа Νν Ню … Википедия
Лямбда (символ) — Греческий алфавит Α α альфа Β β бета … Википедия
Лямбда-барион — Лямбда барионы (Λ барионы, Λ частицы) группа элементарных частиц, представляющих собой барион с изотопическим спином 0, содержащих ровно два кварка первого поколения (u и d кварк). В состав Λ барионов входит ровно один кварк второго или третьего… … Википедия
Лямбда — (Ламбда, Λ, λ) одиннадцатая буква греческого алфавита; как числовой знак 30. Название от семитического lamed острие (жало) … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
лямбда — (др.–греч. Λ, λ λαμβδα) 11 я буква греческого алфавита; с верхним штрихом справа обозначала число 30 , со штрихом внизу слева 30000 … Словарь лингвистических терминов Т.В. Жеребило
Люди (буква) — Буква кириллицы Л Кириллица А Б В Г Ґ Д … Википедия
Альфа (буква) — У этого термина существуют и другие значения, см. Альфа (значения). Греческий алфавит Αα Альфа … Википедия
Читайте также:

